I. Inleiding
Kun je met water kaarsen aansteken? Jazeker!
Is het waar dat slangen bang zijn voor realgar? Nee, dat is niet waar!
Wat we vandaag gaan bespreken is:
Kan interferentie de meetnauwkeurigheid verbeteren?
Onder normale omstandigheden is interferentie de natuurlijke vijand van metingen. Interferentie vermindert de meetnauwkeurigheid. In ernstige gevallen kan een meting zelfs helemaal niet meer normaal verlopen. Vanuit dit perspectief bezien, kan interferentie de meetnauwkeurigheid verbeteren, wat onjuist is!
Is dit echter altijd het geval? Bestaat er een situatie waarin interferentie de meetnauwkeurigheid niet vermindert, maar juist verbetert?
Het antwoord is ja!
2. Interferentieovereenkomst
In combinatie met de feitelijke situatie komen we tot de volgende overeenkomst over de inmenging:
- De interferentie bevat geen gelijkstroomcomponenten. Bij de daadwerkelijke meting bestaat de interferentie voornamelijk uit wisselstroominterferentie, en deze aanname is redelijk.
- Vergeleken met de gemeten gelijkspanning is de amplitude van de storing relatief klein. Dit komt overeen met de werkelijke situatie.
- Interferentie is een periodiek signaal, of een signaal waarvan de gemiddelde waarde nul is binnen een vaste tijdsperiode. Dit is in de praktijk niet altijd het geval. Omdat interferentie echter doorgaans een wisselstroomsignaal met een hogere frequentie is, is de aanname van een gemiddelde van nul voor de meeste interferenties gedurende een langere periode wel redelijk.
3. Meetnauwkeurigheid onder invloed van interferentie.
De meeste elektrische meetinstrumenten en meters maken tegenwoordig gebruik van AD-omzetters, en hun meetnauwkeurigheid is nauw verbonden met de resolutie van de AD-omzetter. Over het algemeen geldt dat AD-omzetters met een hogere resolutie een hogere meetnauwkeurigheid hebben.
De resolutie van AD is echter altijd beperkt. Ervan uitgaande dat de resolutie van AD 3 bits is en de hoogste meetspanning 8V, is de AD-converter equivalent aan een schaal die is verdeeld in 8 segmenten, waarbij elk segment 1V is. Het meetresultaat van deze AD is altijd een geheel getal, waarbij het decimale deel altijd wordt overgedragen of weggegooid. In dit artikel wordt ervan uitgegaan dat het decimale deel wordt overgedragen. Overdracht of weggooien kan meetfouten veroorzaken. Bijvoorbeeld: 6,3V is groter dan 6V en kleiner dan 7V. Het AD-meetresultaat is 7V, wat een fout van 0,7V oplevert. We noemen deze fout de AD-kwantiseringsfout.
Voor het gemak van de analyse gaan we ervan uit dat de weegschaal (AD-omzetter) geen andere meetfouten heeft dan de AD-kwantiseringsfout.
Nu gebruiken we twee identieke weegschalen om de twee gelijkspanningen uit figuur 1 te meten, zowel zonder storing (ideale situatie) als met storing.
Zoals weergegeven in figuur 1, is de werkelijk gemeten gelijkspanning 6,3 V. De gelijkspanning in de linkerfiguur is vrij van storingen en heeft een constante waarde. De rechterfiguur toont de gelijkspanning die verstoord wordt door de wisselstroom, waardoor er een zekere fluctuatie in de waarde optreedt. De gelijkspanning in de rechterfiguur is gelijk aan de gelijkspanning in de linkerfiguur na eliminatie van het storingssignaal. Het rode vierkant in de figuur geeft het conversieresultaat van de AD-converter weer.

Ideale gelijkspanning zonder storingen
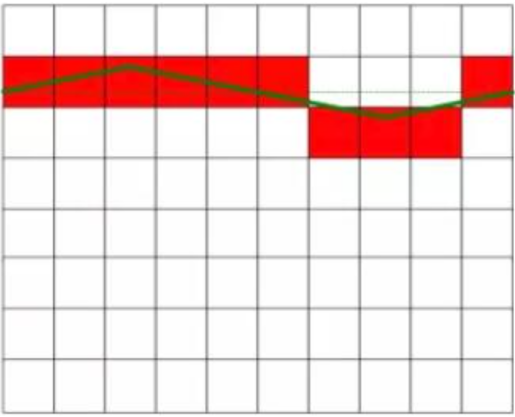
Breng een storende gelijkspanning aan met een gemiddelde waarde van nul.
Voer in beide gevallen in de bovenstaande afbeelding tien metingen uit van de gelijkstroom en bereken vervolgens het gemiddelde van deze tien metingen.
De eerste schaal aan de linkerkant is 10 keer gemeten en de meetwaarden zijn elke keer hetzelfde. Door de invloed van de AD-kwantiseringsfout is elke meting 7V. Na het middelen van de 10 metingen is het resultaat nog steeds 7V. De AD-kwantiseringsfout is 0,7V en de meetfout is 0,7V.
De tweede schaalverdeling aan de rechterkant is drastisch veranderd:
Door het verschil in de positieve en negatieve waarde van de interferentiespanning en de amplitude, is de AD-kwantiseringsfout verschillend op verschillende meetpunten. Onder invloed van deze AD-kwantiseringsfout varieert het AD-meetresultaat tussen 6V en 7V. Zeven van de metingen gaven 7V aan, slechts drie gaven 6V aan, en het gemiddelde van de 10 metingen was 6,3V! De fout is dus 0V!
In feite is geen enkele fout onmogelijk, want in de objectieve wereld bestaat er geen strikte 6,3V! Er zijn echter wel degelijk:
In het geval van geen interferentie, aangezien elk meetresultaat hetzelfde is, blijft de fout na het middelen van 10 metingen onveranderd!
Bij een geschikte hoeveelheid interferentie, na het middelen van 10 metingen, wordt de AD-kwantiseringsfout met een factor tien verminderd! De resolutie wordt met een factor tien verbeterd! Ook de meetnauwkeurigheid wordt met een factor tien verbeterd!
De belangrijkste vragen zijn:
Is het hetzelfde als de gemeten spanning andere waarden heeft?
Lezers kunnen de afspraak over interferentie in het tweede deel volgen, de interferentie uitdrukken met een reeks numerieke waarden, de interferentie over de gemeten spanning heen leggen en vervolgens de meetresultaten van elk punt berekenen volgens het carry-principe van de AD-converter. Daarna kan de gemiddelde waarde worden berekend ter verificatie. Zolang de amplitude van de interferentie de meetwaarde na AD-kwantisering kan beïnvloeden en de bemonsteringsfrequentie hoog genoeg is (veranderingen in de interferentieamplitude volgen een overgangsproces, in plaats van slechts twee positieve en negatieve waarden), zal de nauwkeurigheid zeker verbeterd worden!
Het kan worden bewezen dat zolang de gemeten spanning geen exact geheel getal is (het bestaat niet in de objectieve wereld), er een AD-kwantiseringsfout zal optreden. Ongeacht hoe groot deze AD-kwantiseringsfout is, zolang de amplitude van de interferentie groter is dan de AD-kwantiseringsfout of groter dan de minimale resolutie van de AD, zal het meetresultaat tussen twee aangrenzende waarden verschuiven. Omdat de interferentie positief en negatief symmetrisch is, zijn de grootte en de waarschijnlijkheid van afname en toename gelijk. Daarom is de kans groter dat een bepaalde waarde verschijnt wanneer de werkelijke waarde dichter bij een andere waarde ligt, en zal de werkelijke waarde na middeling dichter bij een andere waarde liggen.
Dat wil zeggen: de gemiddelde waarde van meerdere metingen (waarbij de gemiddelde interferentiewaarde nul is) moet dichter bij het meetresultaat zonder interferentie liggen. Met andere woorden, door gebruik te maken van een wisselstroominterferentiesignaal met een gemiddelde waarde van nul en meerdere metingen te middelen, kunnen de equivalente AD-kwantiseringsfouten worden verminderd, de AD-meetresolutie worden verbeterd en de meetnauwkeurigheid worden verhoogd!
Geplaatst op: 13 juli 2023




